How bad is a Linear Probability Model?

Consistent estimation of the Linear Probability Model (LPM) is difficult and estimates are often biased. Despite these downsides might LPM still be worthwhile? We investigate.

R / statistics

I think a lot about predicting/forecasting binary outcomes. Will the economy head into a recession next year? What’s the likelihood of a loan defaulting over the next few years? Will my followers on social media abandon me if I tweet about my lunch?

One often maligned, but seemingly irresitable approach to modeling binary ourcomes is the Linear Probability Model (LPM). As is known going back to before I was born, the Linear Probability Model has some issues. In particular, it is biased and inconsistent. But is it all that bad? Let’s take a look.

Here are a couple of handy references.

References

Amemiya, T. (1977). Some theorems in the linear probability model. International Economic Review, 645-650. JSTOR

Horrace, W. C., & Oaxaca, R. L. (2006). Results on the bias and inconsistency of ordinary least squares for the linear probability model. Economics Letters, 90(3), 321-327. pdf

Setup

We’re going to keep things simple here and follow the setup in Horrace and Oaxaca. We have a binary (0,1) outcome y that depends on a single regressor x.

The random variable \(x_i\beta\), our regressor times a coefficient falls in three intervals with the following probabilities:

\[ \begin{cases} PR(x_i\beta>1) = \pi,\\ PR(x_i\beta \in [0,1]) = \gamma,\\ PR(x_i\beta>1) = \rho \end{cases}\]

And the LPM is given by:

\[ \begin{cases} Pr(y_i =1 | x_i\beta>1) = 1, \\Pr(y_i=1|x_i\beta \in[0,1],= x_i\beta, \\Pr(y_i =1 | x_i\beta<0)=0 \end{cases}\]

Let’s draw a little picture using R.

library(tidyverse, quietly=T) 
library(ggridges, quietly=T) 
library(extrafont, quietly=T)
c0       <- 0  #intercept for process
beta_hat <- 0.4
gamma_hat <- pnorm((1-c0)/beta_hat) - pnorm(-c0/beta_hat)
rho_hat <- 1-pnorm((1-c0)/beta_hat)
pi_hat <- pnorm(-c0/beta_hat)


df <- 
  data.frame(x=seq(-3,3,.01)) %>%
  mutate(p=pnorm(x/beta_hat+c0),
         shade=ifelse( beta_hat*x >= -1 & beta_hat*x <=1,p,NA))


  ggplot(data=df, aes(x=x,y=dnorm(x), fill="2gamma"))+
    geom_line(linetype=2)+
    geom_area(data= . %>% filter(beta_hat*x +c0 <=1, beta_hat*x + c0 >= 0), linetype=2,alpha=0.5)+
    scale_fill_manual(labels=c(expression(pi),expression(gamma),expression(rho)), name="region",
                      values=c(rgb(103,180,75, maxColorValue = 256),"#27408b","red"))+
    geom_area(data= . %>% filter(beta_hat*x + c0 <= 0), aes(y=dnorm(x), fill="1pi"), alpha=0.5)+
    geom_area(data= . %>% filter(beta_hat*x + c0 >= 1), aes(y=dnorm(x), fill="3rho"), alpha=0.5)+
    labs(x="X", y="Pr(X)", title="Likelihood of X",
         subtitle=expression(paste("Given ",beta," = 0.4")),
         caption=bquote(paste("Pr(",pi,")=",.(round(pi_hat,3)),
                              ", Pr(",gamma,")=",.(round(gamma_hat,3)),
                              ", Pr(",rho,")=",.(round(rho_hat,3)))))+
    theme_ridges(font_family="Roboto")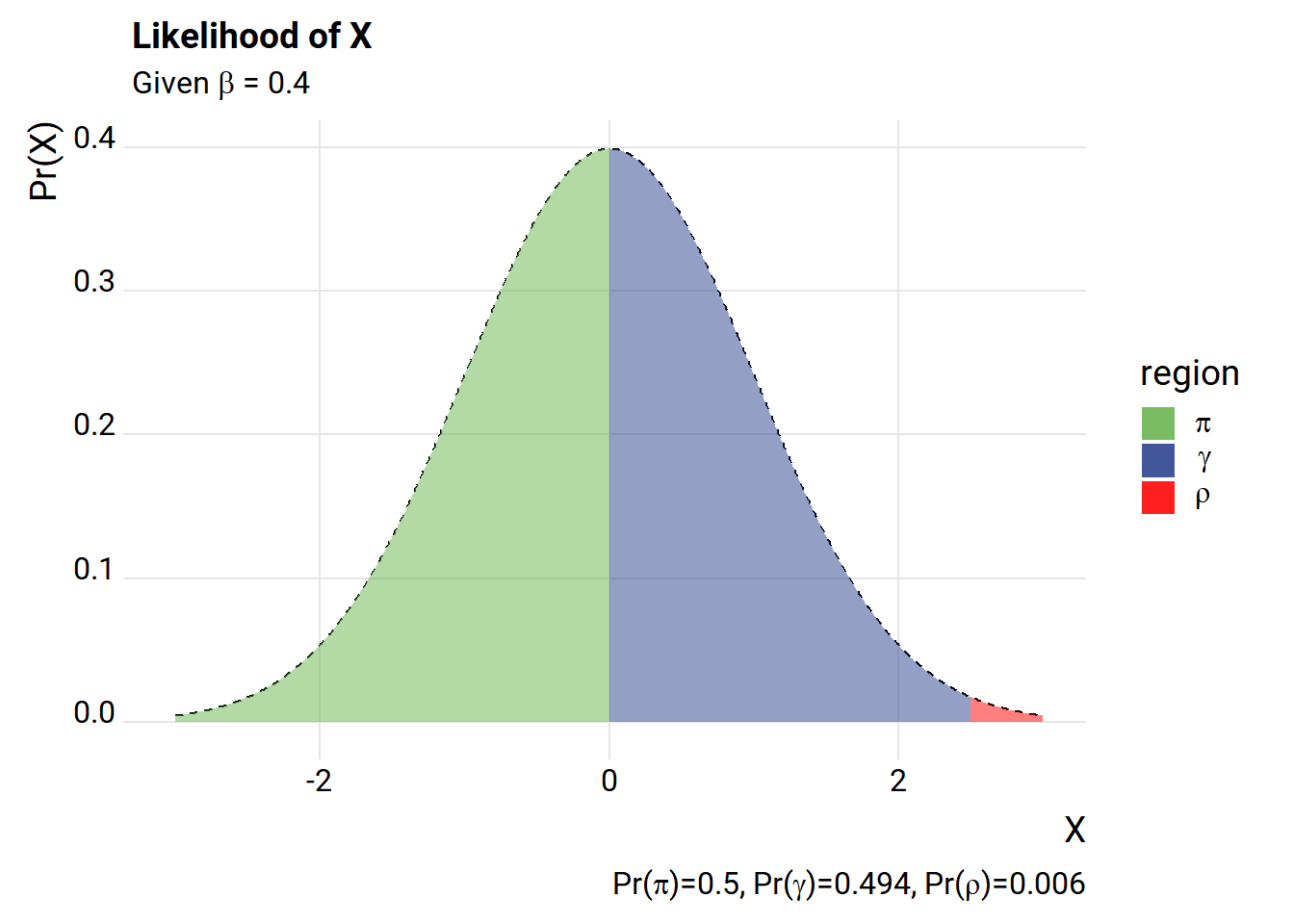

The way we’ve set it up, we have a very high likelihood of drawing an X value that is outside the \(\gamma\) range. Let’s add an intercept.

c0       <- 0.4  #intercept for process
beta_hat <- 0.4
gamma_hat <- pnorm((1-c0)/beta_hat) - pnorm(-c0/beta_hat)
rho_hat <- 1-pnorm((1-c0)/beta_hat)
pi_hat <- pnorm(-c0/beta_hat)


df <- 
  data.frame(x=seq(-3,3,.01)) %>%
  mutate(p=pnorm(x/beta_hat+c0),
         shade=ifelse( beta_hat*x >= -1 & beta_hat*x <=1,p,NA))


  ggplot(data=df, aes(x=x,y=dnorm(x), fill="2gamma"))+
    geom_line(linetype=2)+
    geom_area(data= . %>% filter(beta_hat*x +c0 <=1, beta_hat*x + c0 >= 0), linetype=2,alpha=0.5)+
    scale_fill_manual(labels=c(expression(pi),expression(gamma),expression(rho)), name="region",
                      values=c(rgb(103,180,75, maxColorValue = 256),"#27408b","red"))+
    geom_area(data= . %>% filter(beta_hat*x + c0 <= 0), aes(y=dnorm(x), fill="1pi"), alpha=0.5)+
    geom_area(data= . %>% filter(beta_hat*x + c0 >= 1), aes(y=dnorm(x), fill="3rho"), alpha=0.5)+
    labs(x="X", y="Pr(X)", title="Likelihood of X",
         subtitle=expression(paste("Given ",beta," = 0.4, intercept=0.4")),
         caption=bquote(paste("Pr(",pi,")=",.(round(pi_hat,3)),
                              ", Pr(",gamma,")=",.(round(gamma_hat,3)),
                              ", Pr(",rho,")=",.(round(rho_hat,3)))))+
    theme_ridges(font_family="Roboto")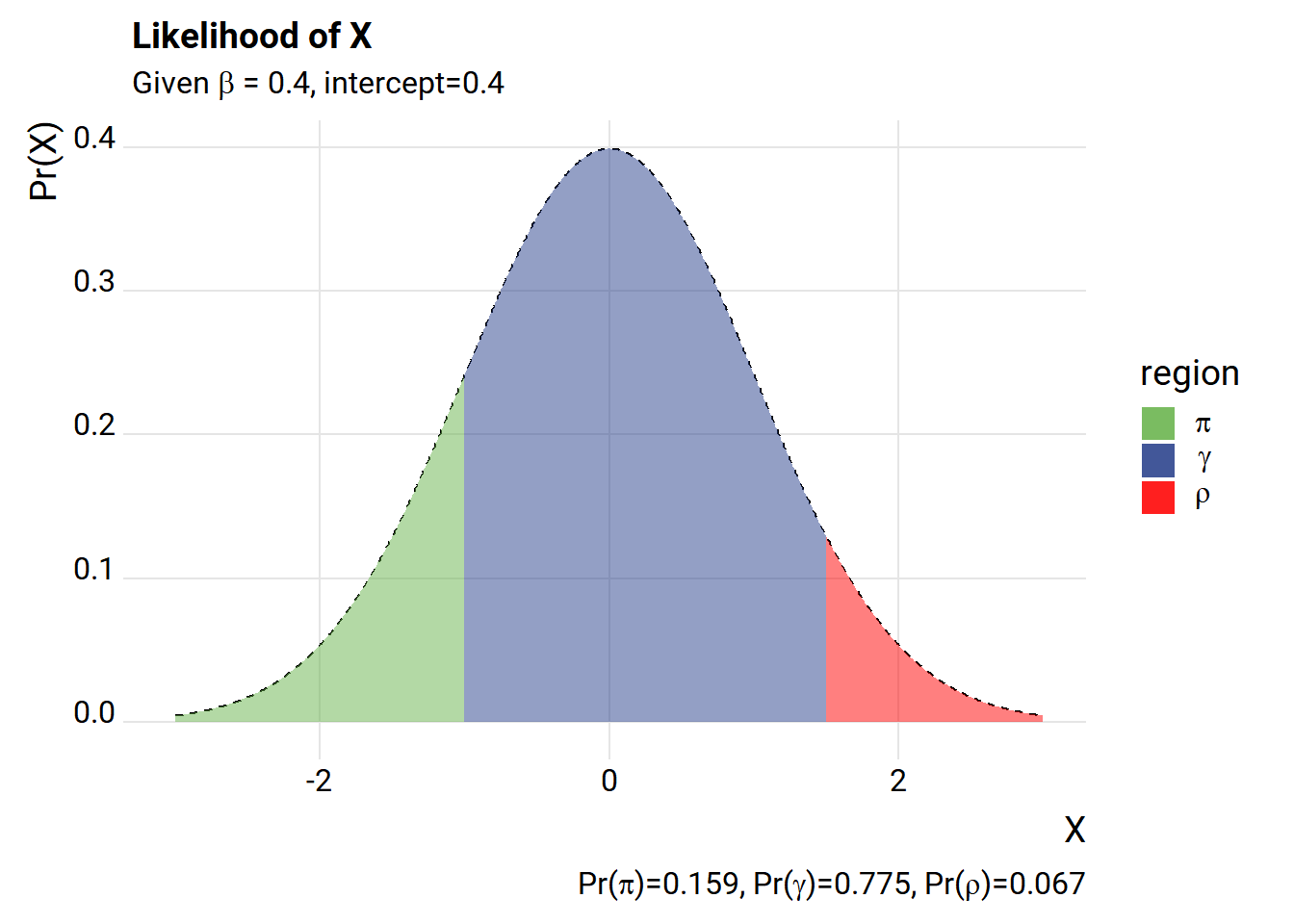

What happens if we simulate some data drawing from the process above and then estimate the LPM using Ordinary Least Squares (OLS)?

Simple simulation

  #helper function to truncate values at 0,1
 myf<- function(x){ case_when(
    x < 0  ~ 0,
    x >  1 ~ 1,
    TRUE ~ x)}

# Simulate under LPM
set.seed(180717)  
c0       <- 0.4  #intercept for process
  beta_hat <- 0.4
  N <- 1000
  X <- rnorm(N)
  z <- c0+beta_hat*X
  Z0 <- myf(z) 
  y <-  rbinom(N, size=1, prob=Z0)
  
  df.reg <- data.frame(y=y,x=X)
  summary(lm(data=df.reg, formula= y~x))
## 
## Call:
## lm(formula = y ~ x, data = df.reg)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.85239 -0.31453 -0.01109  0.30487  0.85901 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.42063    0.01212   34.70   <2e-16 ***
## x            0.31511    0.01222   25.79   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3833 on 998 degrees of freedom
## Multiple R-squared:  0.3999, Adjusted R-squared:  0.3993 
## F-statistic: 665.1 on 1 and 998 DF,  p-value: < 2.2e-16

The true parameter values were 0.4 for both the intercept and the slope \(\beta\). Maybe we got a bad draw? Let’s simulate a number of draws.

We’ll create a helper function and use purrr::map and broom::tidy to help organize the results.

  myreg <- function(N=10){
    X <- rnorm(N)
    z <- c0+beta_hat*X
    Z0 <- myf(z) 
    y <-  rbinom(N, size=1, prob=Z0)
    df.reg <- data.frame(y=y,x=X)
    broom::tidy(lm(data=df.reg, formula= y~x))
  }

# create samples of size 10, 100 and 1000, 1000 draws of  each
  
reg.df <- expand.grid(N=c(10,100,1000), trials=1:100)
suppressMessages(suppressWarnings(  
reg.out <- 
  reg.df  %>% 
  mutate(lm=map(N,myreg)) %>% 
  mutate(map(lm,broom::tidy)) %>%
  unnest(lm)   %>%
  select(N,trials,term,estimate)
))
#create summary table
reg.out %>% 
  group_by(N,term) %>% 
  summarize(ols.mean=mean(estimate),
            ols.median = median(estimate)) %>%
  mutate_if(is.numeric,round,3) %>% 
  mutate(true.parameter=0.4) %>%
  arrange(term) %>%
  htmlTable::htmlTable(caption="Mean/median over 100 trials of size N", css.cell = "padding-left: .5em; padding-right: .2em;", rnames=FALSE)
Mean/median over 100 trials of size N
N term ols.mean ols.median true.parameter
10 (Intercept) 0.418 0.41 0.4
100 (Intercept) 0.422 0.422 0.4
1000 (Intercept) 0.421 0.421 0.4
10 x 0.343 0.342 0.4
100 x 0.309 0.308 0.4
1000 x 0.311 0.311 0.4

Mean/median over 1,000 trials of size N

We see that the coefficients are quite biased, and as pointed out in Horrace and Oaxaca seem to get worse with larger sample size!

Trimming the estimates

Horrace and Oaxaca point out that trimming the estimates, removing observations when \(x_i\beta\) falls outside (0,1), may improve the estimates. Let’s give it a try.

# Function for trimmed estimates

  myreg.trim <- function(N=10){
    X <- rnorm(N)
    z <- c0+beta_hat*X
    Z0 <- myf(z) 
    y <-  rbinom(N, size=1, prob=Z0)
    df.reg <- data.frame(y=y,x=X)
    #first stage
    out.lm <- lm(data=df.reg, formula= y~x)
    df.reg.trim <- df.reg[(predict(out.lm)>=0 & predict(out.lm)<=1 ),]
    out <-     broom::tidy(lm(data=df.reg.trim, formula= y~x))
    out$N.trim <- sum(predict(out.lm)>=0 & predict(out.lm)<=1 )
    return(out)
  }

 reg.df <- expand.grid(N=c(10,100,1000), trials=1:100)
 
suppressMessages(suppressWarnings(  
  reg.out2 <- reg.df  %>% 
    mutate(lm=map(N,myreg)) %>% 
    mutate(map(lm,broom::tidy)) %>%
    mutate(lm.trim=map(N,myreg.trim)) %>% 
    unnest(lm,lm.trim)   %>%
    select(N,trials,term,estimate, term1, estimate1)
))  

reg.out2 %>% group_by(N,term) %>% 
    summarize(ols.mean=mean(estimate),
              ols.median = median(estimate),
              trimmed.mean=mean(estimate1),
              trimmed.median = median(estimate1))%>% 
  mutate(true.parameter=0.4) %>%
  mutate_if(is.numeric,round,3) %>% 
  arrange(term) %>%
  htmlTable::htmlTable(caption="Mean/median over 100 trials of size N", css.cell = "padding-left: .5em; padding-right: .2em;", rnames=FALSE)
Mean/median over 100 trials of size N
N term ols.mean ols.median trimmed.mean trimmed.median true.parameter
10 (Intercept) 0.412 0.416 0.39 0.376 0.4
100 (Intercept) 0.419 0.421 0.398 0.395 0.4
1000 (Intercept) 0.422 0.422 0.405 0.406 0.4
10 x 0.321 0.318 0.483 0.439 0.4
100 x 0.311 0.308 0.384 0.38 0.4
1000 x 0.309 0.309 0.381 0.381 0.4

Seems to work a little better.

We’ll pick back up later with some additional analysis. In particular, I’m interested in studying how the bias changes given the distribution of X. If the likelihood of \(x_i\beta\) falling outside of the (0,1) range is zero, then the bias goes away. I’m also interested in looking at how aggregations over the LPM model behave.

Despite the defects in the LPM I still feel it has some strengths. Not only are the marginal effects more easily interpretable but it’s also easier to aggregate.

Are those advantages enough to overcome the disadvantages? That’s going to depend on the context. Next time we’ll explore some cases where it might be worthwhile.

 Share!